Maximum Subarray Sum

Problem

Calculate the maximum sum present of consecutive elements in an array

BruteForce Solution

​​

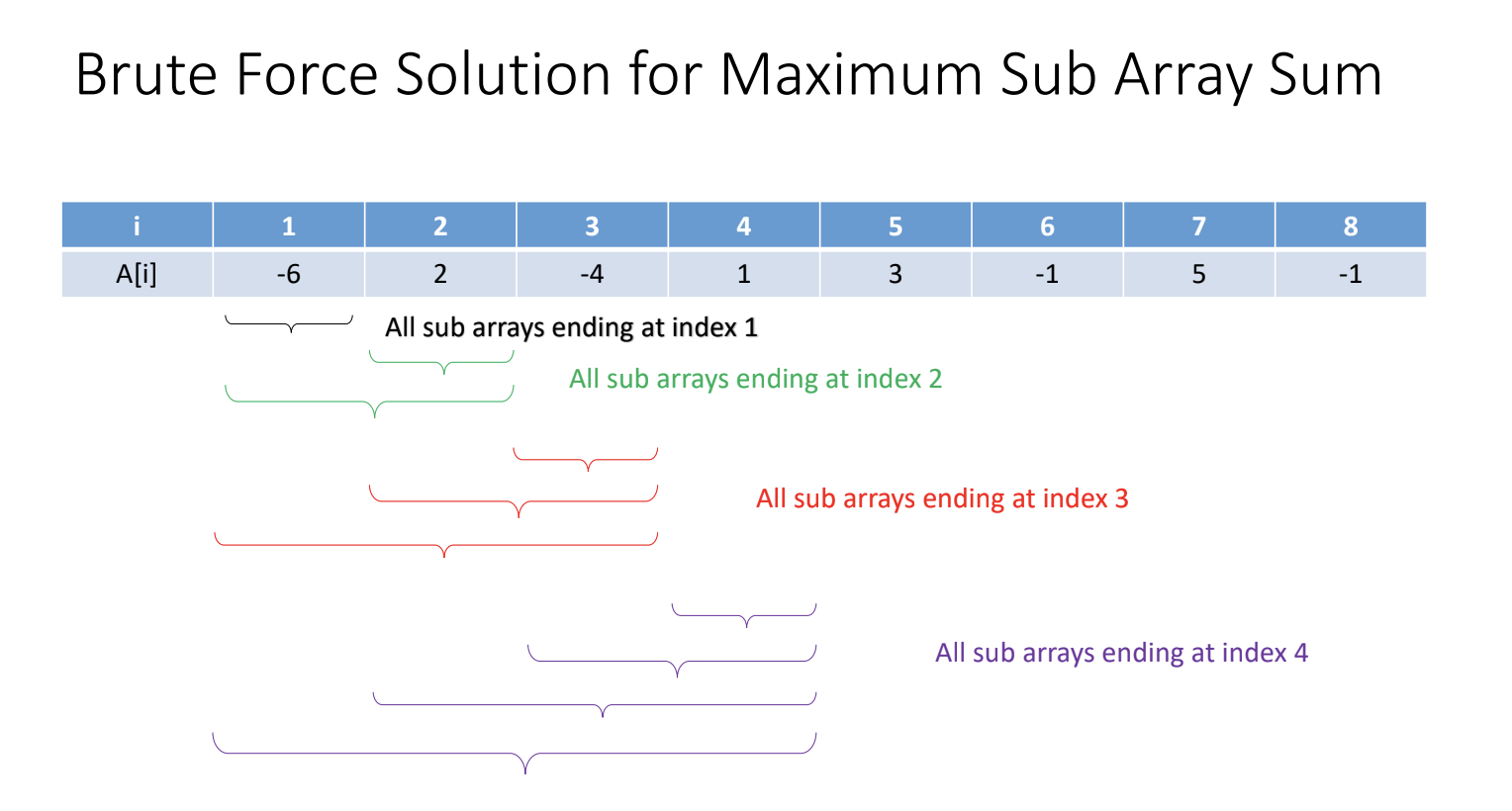
int arr[] = {-6, 2, -4, 1, 3, -1, 5, -1};
int indx[] = {0, 0};
int size = 8;
 
int maxSum = 0;
for(int i=0; i<size; i++){ // Controls the From Index
	int sum = 0;
	for(int j=i; j<size; j++){ // Controls the Till Index - Increases
		sum += arr[j];
		if (maxSum < sum){
			maxSum = sum;
			indx[0] = j;
			indx[1] = i;
		}
	}
}
 
cout << "MaxSubArray Sum: " << maxSum << endl;
cout << "From Index " << indx[0] << " To " << indx[1] << endl;

**Complexity: ** $\theta (n^2)$

Divide and Conquer Solution

​​

MaxSubArraySum(A, l, r){
	if (l == r) return array[l]
	m = (l+r)/2
	return Max  [ MaxSubArraySum(A, l, m)
				  MaxSubArraySum(A, m+1, r)
				  MaxCrossingSum(A, l, m, r) ]
}

We follow the same recursive approach as that of a Merge Sort but do not actually sort

MaxCrossingSum(A, l, m, r){
	sum = 0

	for(i = m to l )
		sum = sum + A[i]
		leftSum = Max (leftSum, sum)

	sum = 0

	for(i = m+1 to r )
		sum = sum + A[i]
		rightSum = Max (rightSum, sum)

	return leftSum + rightSum
}

The MaxCrossingSum​​​ function gets two arrays and is responsible for finding the max sum from both of them individually, but the consecutive elements to sum are logically connected to middle of the both array combined. Means that for left array, the elements to be considered for summation should be consecutive combinations from end of the array to left and as for the right array, they should be from start of the array to the end. Then the function further sums the two sum, logically returning a crossing sum.