Rod Cutting Problem

Problem Statement

Some company buys long steel rods and cuts them into shorter rods, which it then sells.

Each cut is free. The management of company wants to know the best way to cut up the rods.

We assume that we know the price p_i in dollars (for i = 1, 2,…n ), that the company charges for a rod of length i inches. Rod lengths are always an integral number of inches.

Goal

Determine the maximum revenue r_n , obtainable by cutting up the rod and selling the pieces

Example

Length i	1	2	3	4	5	6	7	8	9	10
Price pi	1	5	8	9	10	17	17	20	24	30

​​

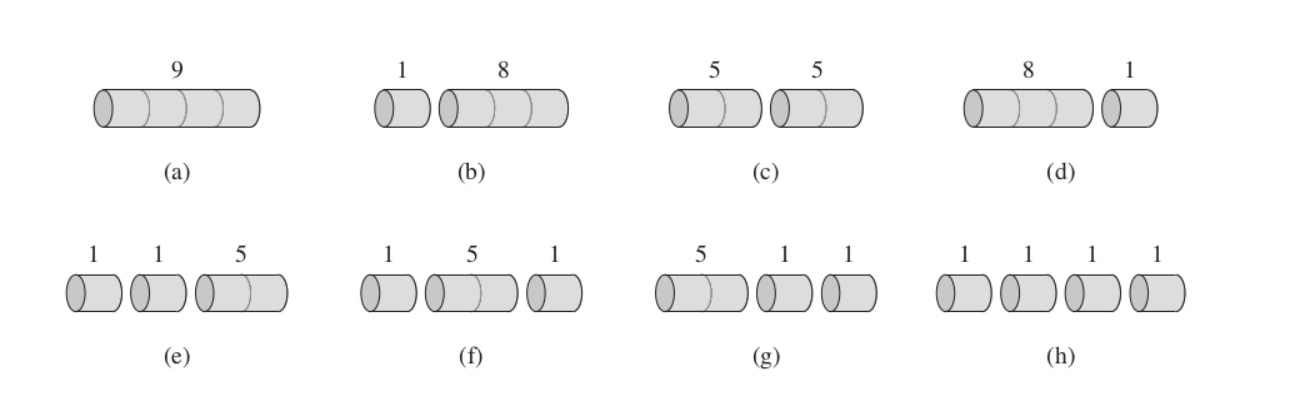
The most optimal revenue will be deduced by cutting the rod into 2 equal cuts: 5+5 = 10

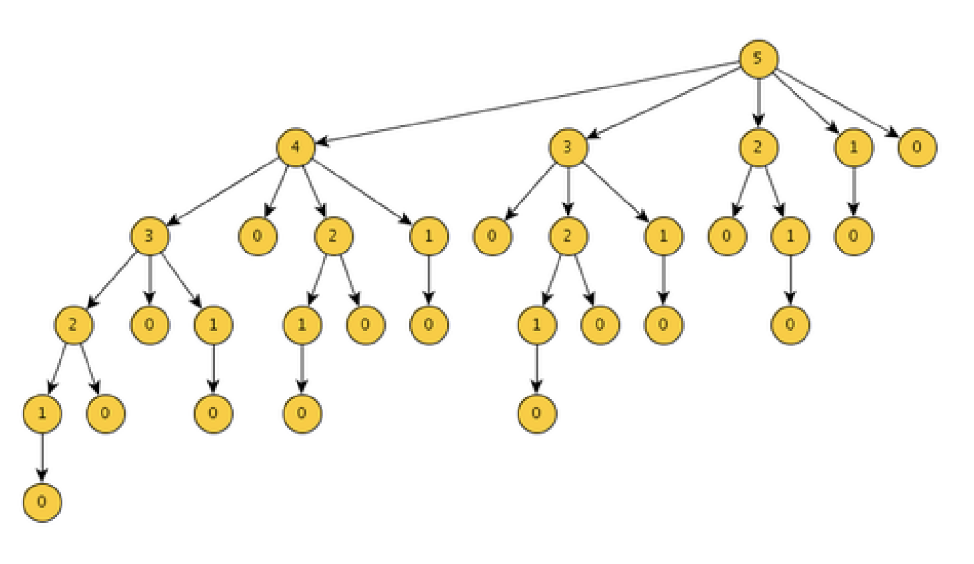
Brute Force Solution

We will explore each possibility of cutting the rod into various sizes

This can be defined from the recurrence:

$$r_n=ma{x}_{1\le i\le n}(p_i+r_{n-i})$$

• Cut a piece of length i , with remainder of length n

• Only the remainder, and not the rest piece, may be further divided

  • Hence only the remainder is being used to check the optimal solution of rest of the length

​​

This Solution will give us a Time Complexity of T(2ⁿ )

This is because every recursive call itself produce further n-1 recursive calls

​​

Dynamic Programming Solution

Optimal Substructure

• The Optimal Solution / split of the current length can also have an optimal solution

​​

Memoization

• We can avoid repetitions through memoization

​​

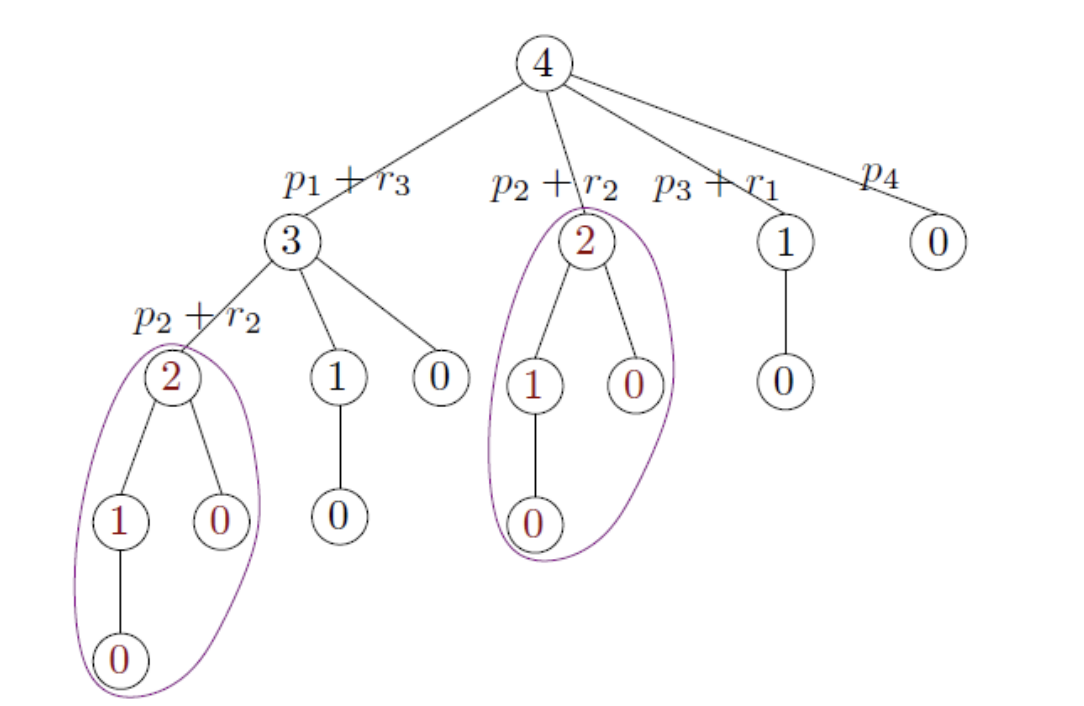
To implement this we can just change the notation of our BruteForce Recurrence

$$r[n]=ma{x}_{1\le i\le n}(p[i]+r[n-i])$$

We can store the result / revenue r​ into an array

Bottom Up DP Solution

​​

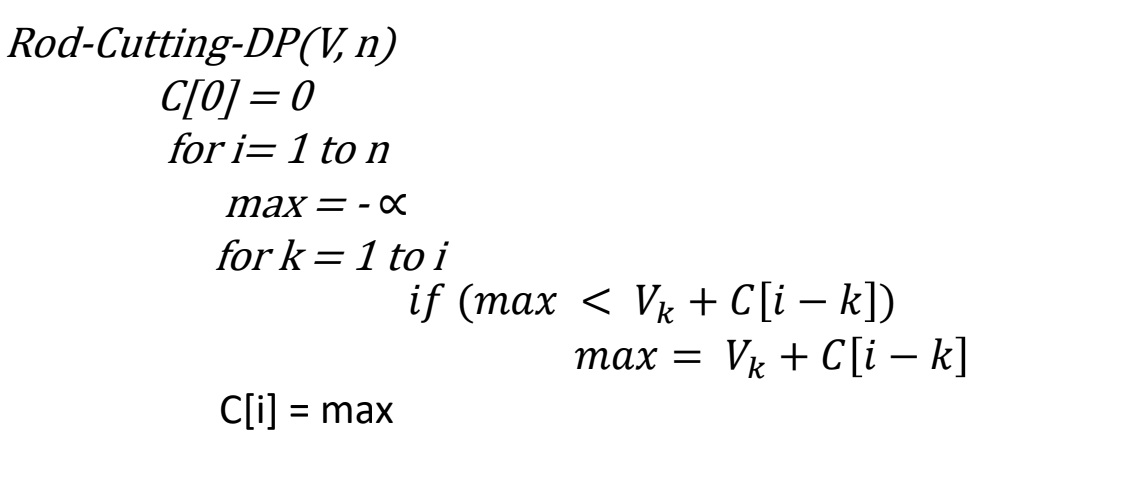
Where C is our array r​ and V is the array p​

This give us a Time Complexity of $n^2$